How Formal Verification of Smart Contracts Works
Runtime Verification Inc provides Formal Smart Contract Verification services.
In this post, we'll describe – in general terms – the process of verifying a smart contract. Later posts in this series will provide more detail, contrast verification to other automated ways of increasing assurance, and cover other topics.
The pieces that matter for testing
Let's look at what any sort of verification has to work with, starting here:

A smart contract is written in a programming language (commonly Solidity) and then translated into bytecodes. Once a smart contract is reduced to bytecodes, it can be deployed on the blockchain as a contract account at some address. An address is a huge number (for reasons irrelevant to this post.)
In the following example, our contract has been deployed at address 0x4ab05eaa0451ec006210810947b598f59824dec483b187028620ca168edd6a9e (0x4ab05 for short.)
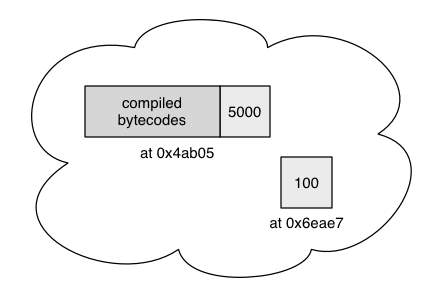
A contract account contains funds, a compiled contract, and other data.
The picture also shows an externally owned account (at 0x6eae7). Such an account contains only funds (100 ether in this case).
A contract begins working after a transaction addressed to it is submitted to the network. Here's a transaction that transfers ether from the submitter's account to another account:
transfer(4000 ether, address(0x6eae7))
That transaction will be performed by potentially thousands of computers (miners) all executing a copy of the same virtual machine (VM). The VM interprets the transfer function's bytecodes, which will instruct it (in this case) to subtract 4000 ether from 0x4ab05 and add it to 0x6eae7.

Because all the VMs are processing the same data with the same bytecodes, they'll all produce the same answer.
What we want
Our goal is to have great confidence that the contract will behave correctly no matter what value is to be transferred, no matter what the balances of the two accounts, and no matter which account is to receive the value.
There are various ways we could fail to get what we want.
-
The programmer could misunderstand the intent. For example, suppose no one said what to do if there wasn't enough money to transfer. Should the
transferfunction fail? Or should the contract make a "best effort" and transfer only what was available?The programmer might assume one – the wrong one – is the "obvious" choice and implement it.
-
The programmer might know what was needed but make a mistake when implementing the intent. For example, the Hackergold exploit was due to mistyping
+=as=+."If builders built houses the way programmers build programs, the first woodpecker to come along would destroy civilization." – Jerry Weinberg
-
The virtual machine is a program, so it can contain either one of the above flaws. VM bugs are less common but can be serious.
Auditing and testing find bugs, so they increase confidence. We'll leave auditing aside, and compare it to formal verification in a later post. For this post, testing makes for a better comparison.
An experienced tester would check a list of conditions like these:
- transfer zero ether
- transfer all the ether
- transfer slightly more than all the ether
- transfer the largest possible amount of ether (hoping to discover overflow bugs)
- transfer an account's value to itself
- ...
The tester would turn that into tests by picking specific values for each bullet point. (You can't just "transfer all the ether" – you have to pick a specific number for both the contract and receiver's starting balances, and you need to provide transfer with a specific address.) Running a test means predicting the final balances, making the transfer, and checking if what the contract actually did is the same as what it should have done.
How well this process works depends on how easily the contract can get the right result for the wrong reason. As a simple example not involving smart contracts, suppose you were testing addition and tried two cases: 0, 0 and 2, 2. The code correctly produces 0 and 4, so you conclude it's correct. But what if addition was mistakenly implemented as multiplication? The tests still pass, but you – bad luck! – happened to choose the only two tests that would.
In the case of addition, it'd be hard to actually miss the problem. In other cases – especially error handling – it's much easier. You can think of formal verification as a way to eliminate certain kinds of bad luck.
What is formal verification?
Mathematicians are in the business of looking at things like this:

... and noticing commonality:
- The cube has and 6 faces, 12 edges, and 8 pointy bits.
- The tetrahedron has 4 faces, 6 edges, and 4 vertices.
- In both cases, the number of faces plus vertices is two more than the number of edges.
Mathematicians then ask the same question we should have asked with our two addition tests: is this an accident, or is it always true? And they've discovered ways of being really, really confident that something is always true. Those ways are lumped together under "proofs and proof techniques."
(I say "really, really confident" instead of "absolutely sure", because people can still make mistakes. One mistake is failing to notice special cases. For example, the rule above doesn't work for shapes with holes in them. We'll see the relevance of this observation later.)
Given the success of mathematics over the past few thousand years, it's natural to want to apply proof techniques to the question of "does this program always do what it should?"
What extra pieces does formal verification need?
If we're to prove that a program always does what it should, we have to be precise about what "should" means. That's called the contract's specification:

With a specification, a human can take any specific set of starting values (arguments to transfer, balances and addresses of accounts), and a set of ending values, then determine if they match the specification.
This differs from the expected results of a test in that a test works only on a single set of starting values, whereas a specification will work for any set.
A formal specification is one that's precise and exact enough that a computer can do the checking. Such specifications can be daunting to read. What follows is the formal specification for the balance method, as written in the K language. (transfer is more complicated.)

Creating a formal specification is very much a manual process, and the task requires considerable expertise. It's not cheap, but it's necessary for formal verification. As a bonus, it's not unusual for the required rigor to uncover mistakes in an informal specification. In our work verifying ERC20 contracts, we found cases the ERC20 informal specification didn't address.
Formal verification could compare the Solidity contract against the Solidity specification. Instead, Runtime Verification works with the bytecodes. There are three reasons for that:
-
A great deal of up-front work (see below) has to be done for each language. Work done for Solidity would be of no help with, for example, Plutus. But once the work has been done for the bytecode language, it can be used for any high-level contract language.
-
It allows stronger verification. Many exploits are based on quirks of the virtual machine like stack size limits or gas calculations. Such exploits couldn't be ruled out with Solidity-level verification.
-
The Solidity compiler could have a bug. If it produces the wrong bytecodes for a correct contract, that can only be caught by verifying bytecodes.
Working at the bytecode level has a cost, though. The Solidity specification has to be refined with virtual machine details:

Because of the technical intricacies of the translation, it has to be done manually today. We'll be adding automated support in the future.
In order to check that the contract's bytecodes matches its specification, we need to know what each bytecode does and the bit-level structure of the data it works on. That is, we need a specification (or semantics) for the virtual machine:

Creating such a semantics is quite labor-intensive, but it only has to be done once for any given virtual machine.
Time to verify
At this point, we can ask an automated theorem prover (in our case a part of the K verification framework) to use the semantics to prove that the compiled contract implements the specification:

In a perfect world, we'd get one of two messages from the prover:
- "I created the proof that the contract is right."
- "The contract is wrong."
In our world, the prover sometimes can't do either. It needs hints and other help from a human:

Proving a contract is thus an iterative process where the prover tries and gets stuck, a skilled human gets it past the current sticking point, the prover tries again, and so on.
A success story
Some financial calculations require raising a number to a power. One contract that failed to prove correct used such a pow function. To understand the problem, consider the following use:
pow(0.1, 21)
That raises a small number to a large power. The result is a very small positive number, specifically 0.000000000000000000001.
Later in the contract, that result of pow is divided into another value. Let's suppose that other value is 3. The result is a very large number (3000000000000000000000). That's not unrealistic: in the basic unit of the Ethereum blockchain ("wei"), that's only 3000 ethers.
All seems well, but this contract used fixed-point numbers (numbers that only support a fixed number of digits past the decimal point). That means that 0.000000000000000000001 might be too small to fit, in which case it would be rounded to zero.
What's 3/0? In many languages, that's a drastic failure. (The contract wouldn't complete.) In the EVM version of Solidity, it's zero. The result? A contract that should have processed 3000 ether processed none.
That could be bad.
Honesty compels us to admit that it would take several hundred years for this particular contract to fail for this reason. But pow plus fixed-point numbers is an exploit waiting to happen. Somewhere, some contract programmer won't know the danger, or will momentarily forget it, or mistakenly think that small numbers can't get to pow. The justification for formal verification is that the prover won't fail in any of those ways.
Let's take stock
When a whole contract is proven, four new documents (two specifications, one VM semantics, and a set of hints) plus one new tool (the prover) have given us confidence beyond what we could have gotten from testing. What risks remain? In particular, how could the worst case happen: we think the compiled bytecodes are correct, we deploy them to the blockchain, and it turns out they weren't correct in some way that makes them vulnerable to an exploit.
- The prover is a program, and programs have bugs. It's possible that a previously unnoticed bug could be just the one to make the prover accept your contract when it shouldn't have. Only one such bug has ever been detected in K, though.
In the future, K will be enhanced to generate machine-checkable proofs. Either Runtime Verification or a third party could implement a proof checker to serve as an automated auditor of proofs. A proof checker is much simpler and smaller than K. We estimate its core logic will probably be a few hundred lines of code.
-
The virtual machine semantics might not match the actual virtual machine. They'd have to be wrong in just the right way to let a bad contract slip by, which is unlikely. (Still, our approach to the problem is to avoid it entirely by generating the VM from its specification. That doesn't apply to the EVM, which was written independently of its specification.)
-
The Solidity specification could be wrong. A specification's author can get intent wrong, just as a programmer can. A prover won't notice that the code faithfully implements the wrong behavior for an overdrawn account – in fact, it will insist on the wrong behavior.
Similarly, if the specification says nothing about logging, any logging behavior will be fine with the prover.
This problem – of translating people's thoughts into symbols a computer can work with – will always be with us.
-
The specification may omit relevant domain knowledge. When verifying ERC20 smart contracts, we found that we needed to separately describe the case where ether was being transferred to the same address it came from. If we'd overlooked that case, the prover would have too. (In the case of one ERC20 contract we verified, that would have meant the prover missed a bug. It's a minor bug, but it could have been worse.)
Here the specification-writer runs into the same problem as the tester: it takes experience to reliably think of all the cases. However, this is where working in a restricted domain like smart contracts gives formal verification an advantage. There's no technical reason that the fact an address has a special case can't be codified in a way the prover can use. It just hasn't been done yet. Once it has, the prover will never overlook it, unlike a human tester.
Other special cases have been codified. The virtual machine semantics describe arithmetic overflow. The specification writer can forget to think about it, but the prover will still discover overflow bugs.
-
The Solidity specification has to be manually translated into the VM specification. Mistakes can be made. In the future, there will be automated support.
Take these points away
-
Formal verification can reliably detect bugs – like tricky arithmetic overflow or self-transfers – that testing and auditing easily miss.
-
The process requires manual labor, much of it highly skilled and therefore expensive.
-
However, formal verification is practical today. The cost is no greater than a thorough human audit and, we believe, provides greater confidence to both the contract owner and to customers calling into the contract.
-
Smart contracts are a particular, specialized domain. That gives formal verification more leverage. The small size of smart contracts makes full verification cheaper. There are not too many key concepts in the domain, so it is tractable to tailor the tools to it: further reducing cost and increasing effectiveness.
-
There are still a number of easy improvements – low-hanging fruit – that we haven't implemented yet, so future progress should be rapid.